无向树:连通不含回路的无向图,这里所说的回路是简单回路或初级回路
生成树:若无向连通图的生成子图是树,则称其为生成树;图中在生成树上的边称为枝,不在生成树上的边称为弦
最小生成树:无向连通带权图的所有生成树之中权最小的树称为该图的最小生成树
根树:只有一个顶点入度为0,其余顶点入度均为1的非平凡的有向树称为根树
有序树:每一层上的顶点都按照规定次序的根树
r元树:每个分支点最多有r个子节点
正则树:每个分支节点恰好有r个子节点的r元树
完全树:所有树叶的层数恰好为树高
最优二元树:

前缀:

前缀码:符号互不为前缀的符号串集合称为前缀码,特别地,符号串由0,1构成的前缀码称为二元前缀码,二元前缀码可以由二元树产生
最佳前缀码:平均码长最小的二元前缀码称作最佳前缀码,其中平均码长为 ,其中 为各个字符串的长度, 为各个字符串的权重
二叉树节点数目:对于二叉树, ,其中 为二叉树的具有 各子节点的节点数;另一种不同的表示是, ,其中 为二叉树的度为 的节点数;该结论可以推广到多叉树
Kruskal算法(求最小生成树的避圈法):
按照边的长度从小到大拓展边,若待拓展的边与已拓展的边形成环,则放弃拓展该边
Huffman算法(求最优二元树的算法):
将权值最小的两个树叶合成一个新的子树放入待合成序列中,重复合成直到所有的节点都合成一棵树
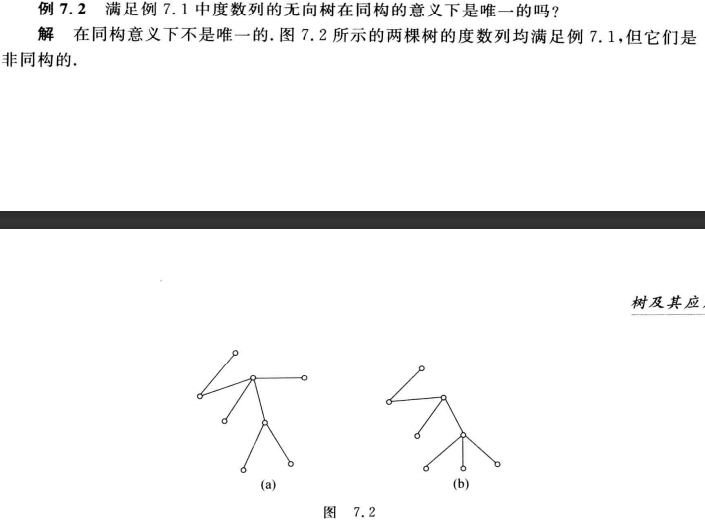
补充:例7.1的度序列为1,1,1,1,1,2,3,4

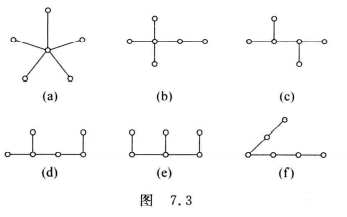
提问:给定度序列,如何确定所有不同构的树?

7.1证明:树都是二部图
7.2证明:除了平凡树外,树都不是欧拉图
7.3证明:除了平凡树外,树都不是哈密顿图
7.4证明:树都是平面图

NP难问题

要注意使用的是哪种节点数目表示方法,是子节点数目还是度
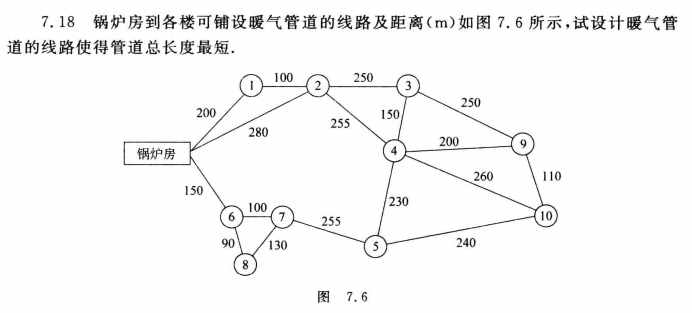
注意:最短总长度就是要求最小生成树,而不是单源最短路径

需要明确关于根树的各种定义:
内点——除了根节点之外的非叶子节点
分支节点——包括根节点的所有非叶子节点
高度——从根节点到最远的叶节点的路径上的边的总数
元数——节点最多的子节点数目

注意:使用握手定理以及等比数列求和公式
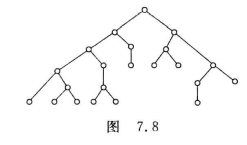
注意:树根到树叶从左到右决定前缀码,不要写反
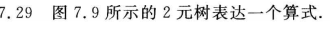

注意:中序遍历序列,对于非叶节点每回溯一次添加一对括号