命题——所表达的判断是真或假但不能既真有假的陈述句
简单命题——陈述句中没有联结词出现,或称不能再分解的命题
复合命题——简单命题通过联结词联结而成的陈述句
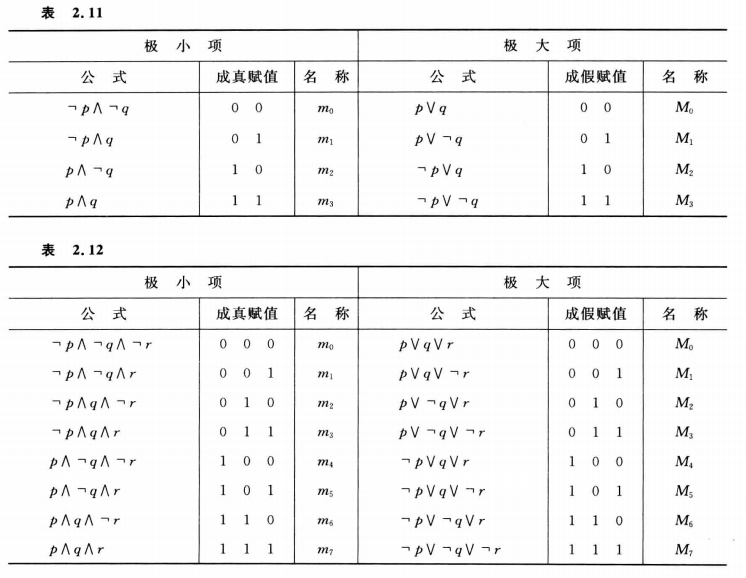
联结词:否定联结词,合取联结词,析取联结词,蕴含联结词,等价联结词
命题常项——简单命题
命题变项——真值可以变化的陈述句
合式公式、命题公式——将命题变项用联结词和圆括号按照一定的逻辑关系联结起来的符号串
重言式——各种赋值下取值均为真的命题公式
矛盾式——各种赋值下取值均为假的命题公式
可满足式——存在赋值使取值为真的命题公式(即非矛盾式)
通过等值式模式从一个公式推出一个与其等值的公式
等值式模式


文字——命题变项及其否定统称作文字
简单析取式——有限个文字构成的析取式
简单合取式——有限个文字构成的合取式
析取范式——由有限个简单合取式构成的析取式称为析取范式
合取范式——由有限个简单析取式构成的合取式称为合取范式
析取范式与合取范式统称为范式
主析取范式——含有n个命题变项的简单合取式中,每个命题变项和它的否定式不同时出现,二者之一出现且仅出现一次,命题变项按顺序出现,简单合取式按照极小项下标从大到小出现
主合取范式——含有n个命题变项的简单析取式中,每个命题变项和它的否定式不同时出现,二者之一出现且仅出现一次,命题变项按顺序出现,简单合取式按照极大项下标从大到小出现
极小项——有限个命题变项或者其否定式之一按照一定顺序出现且仅出现一次的简单合取式
极大项——有限个命题变项或者其否定式之一按照一定顺序出现且仅出现一次的简单析取式
注意:
推理就是一组蕴含式 ,证明推理正确,就是证明这个蕴含式是重言式


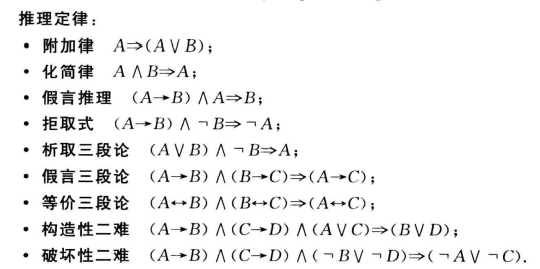
归结规则(其实就是假言三段论)


简单析取式为重言式的充要条件:简单析取式是重言式当且仅当它同时含有某个命题变项及其否定式
简单合取式为矛盾式的充要条件:简单合取式是矛盾式当且仅当它同时含有某个命题变项及其否定式
析取范式是矛盾式的充要条件:一个析取范式是矛盾式当且仅当构成它的每一个简单合取式都是矛盾式,亦即每一个简单合取式都含有某个命题变项及其否定式
合取范式是重言式的充要条件:一个合取范式是重言式当且仅当构成它的每一个简单析取式都是重言式,亦即每一个简单析取式都含有某个命题变项及其否定式
范式存在定理: 任一命题公式都存在与之等值的析取范式与合取范式
范式存在定理以及求范式的步骤

主析取范式与主合取范式存在唯一定理:任何命题公式都存在与之等价的主析取范式和主合取范式,并且是唯一的
求主析取范式与主析取范式的方法:

快速求主析取范式与主合取范式的方法:

主析取范式与主合取范式的应用:
1)求公式成真与成假赋值
2)判断公式类型
3)判断两个命题公式是否等值
4)应用题
判断推理正确性的方法:
(1)真值表
(2)等值演算
(3)主析取范式
(4)观察法,通常观察出成假赋值证明其不是重言式
(5)推理证明
推理正确性的证明方法:
推理正确性可以从公式真值表和命题演算来判断,但在实际应用中,构造推理的证明是基本方法
命题演算和推理证明的区别:
命题演算是从推理的形式结构出发,得到命题是真或假或可满足的;推理证明是从前提出发,通过推理定律得到结论
附加前提证明法:

归谬法:

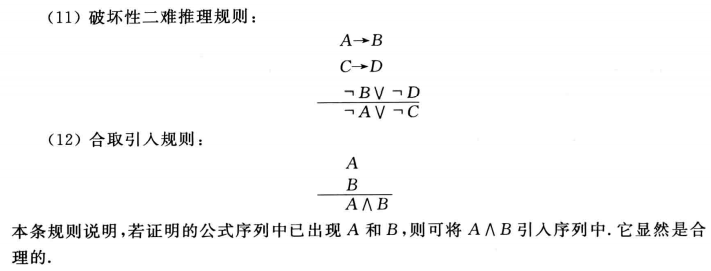
归结证明法:
基本思想是归谬法
步骤如下:
(1)把结论的否定引入前提
(2)把所有的前提,包括结论的否定在内,化成合取范式,并把得到的合取范式中所有的简单析取式作为前提(重复的简单析取式删去)
(3)应用归结规则进行推理
(4)如果推出空简单析取式,即0,则证明推理正确
前提假证明法:若前提为矛盾式,则推理必为真
结论真证明法:若结论为重言式,则推理必为真
间接证明法:
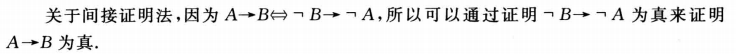
归谬法:否定结论来证明推论错误
分情况证明法:

附加前提证明法例题
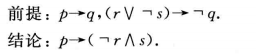

归谬法例题

2.31

采用不同方式求主析取范式的复杂度
方法一,求主合取范式,通过主合取范式求主析取范式。缺点:在命题变项较多的情况下,需要补齐的简单析取式过多,需要消去的重复的简单析取式过多。手算较复杂。
方法二,将简单析取式两两通过分配律化为析取范式,重复直到原命题化为主析取范式。手算相对方法一简单,但是需要注意用分配律合并过程中可能出错。


2.35