一阶逻辑考虑了命题之间得内在联系和数量关系,引入个体词、谓词和两次,以期表达出个体和总体得内在联系和数量关系。
一阶逻辑也称一阶谓词逻辑或谓词逻辑。
个体词指研究对象中可以独立存在的具体或抽象的客体
个体常项——表示具体或特定的个体的个体词称作个体常项
个体变相——表示抽象或泛指的个体的个体词称作个体变项
个体域(论域)——个体变项的取值范围
全总个体域——由宇宙间一切事物组成的个体域,若论述或推理中无指明所采用的个体域,都默认使用全总个体域
谓词——用来刻画个体词性质及个体词之间相互关系的词
谓词常项——表示具体性质或者关系的谓词
谓词变项——表示抽象或泛指的性质或者关系的谓词
0元谓词——不带个体变项的谓词
量词——表示个体常项或变项之间数量关系的词成为量词
全称量词——表示个体域内所有个体具有某种性质
存在量词——表示个体域内存在个体具有某种性质
一阶语言的字母表

项

原子公式

合式公式

指导变元

闭式——公式中不含自由出现的个体变项,则称此公式为封闭的公式,简称闭式
非逻辑符号——一阶语言中个体常项、函数符号和谓词符号称作非逻辑符号,其余符号称作逻辑符号
非逻辑符号集记为L,称一阶逻辑语言为非逻辑符号集L生成的一阶语言,不同的非逻辑符号集生成不同的具体的一阶语言,但他们使用相同的逻辑符号和相同的生成规则。解释是对具体的一阶语言而言的。
解释

永真式——在任何解释和赋值下都为真的公式,也称为逻辑有效式
矛盾式——在任何解释和赋值下都为假的公式,也成为永假式
可满足式——至少存在一个解释和一个赋值使其为真的公式
代换实例——一谓词公式代替命题公式中的命题变项
作用是快速判断一个公式是永真还是永假还是可满足

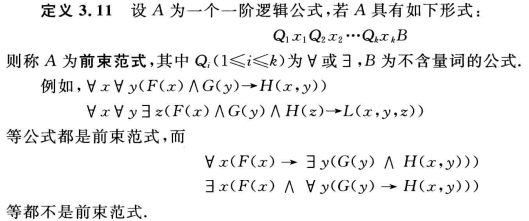
闭式:闭式在任何解释下都成为命题
赋值:进一步,在给定解释后,为公式中每一个自由出现的个体变项制定个体域中的一个元素,则非封闭的公式也变成命题了。
给定解释和赋值,任何公式都变成为命题。
代换实例:重言式的代换实例都是永真式,矛盾式的代换实例都是矛盾式
一阶逻辑等值式

置换规则与换名规则

前束范式存在定理:一阶逻辑中的任何公式都存在与之等值的前束范式


注意:什么时候,在解释下的公式成为命题?——命题是有确定真假的陈述句。


注意:全称量词对析取联结词无分配律,存在量词对合取联结词无分配律