设离散型随机变量 的分布列为 ,则
设 为连续函数或者分段连续函数,则
设连续型随机变量 的密度函数为 ,则
设 为连续函数或者分段连续函数,则
性质
1)
2)
方差定义为
离散型随机变量
对于分布列为 的离散型随机变量 ,
连续型随机变量
对于密度函数为 的连续型随机变量 ,
性质
1)
2) 几乎处处为某个常数 ,即
3)
4)若随机变量 相互独立,则 ,
定义
协方差定义为 ,相关系数定义为
对于联合分布为 的离散型随机变量 ,
对于联合分布的密度函数为 的连续型随机变量 ,
性质
1)
2)
3)
4) 相互独立 ,即独立性可推出不相关性,但反之未必
5)
6)若 ,则 独立 不相关 ,对于正态分布,独立性与不相关性等价
证明性5),需要柯西施瓦茨不等式 ,等号成立当且仅当 ,用判别式法可以证明
用分布判定独立性
随机变量 相互独立,则对任意实数 ,事件 相互独立,即联合分布等于各自的边缘分布相乘
用数字特征判定不相关性
不相关
判定步骤
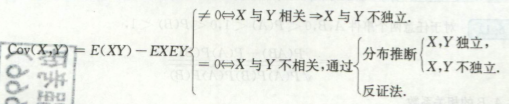
重要结论
1)独立 不相关,相关 不独立
2)对于二元正态分布以及二元0-1分布,独立 不相关
设随机变量 的数学期望和方差存在,则对任意的 ,有
证明:
从而有