一、十进制与二进制相互转换(仅介绍常用方法)
1、整数
除2取余法到0为止
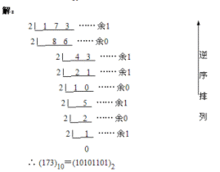
图片来源百度百科
2、小数(有限精度)
小数采用乘2法,每次乘法取整数位值,若为1,则取1的同时将该小数-1,继续乘2直到小数位为0
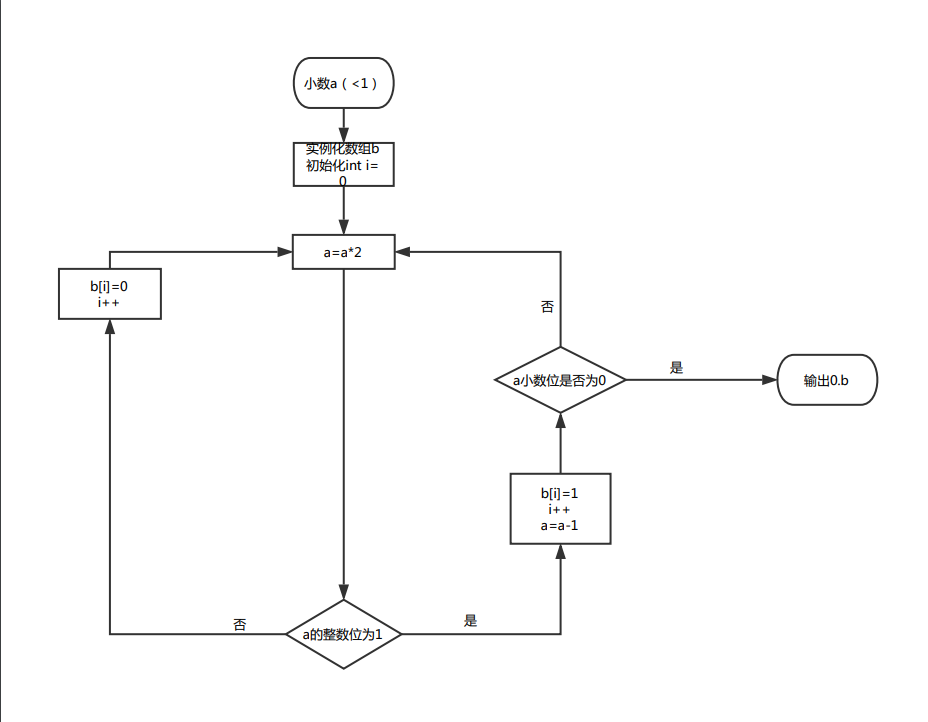
这里使用了一种抽象化程序的方式,0.b指将数组内容放在0.后面
二、float和double数据类型
float4个字节32位,double8个字节64位,其二进制表示结构如下
类型 | 符号位 | 阶码 ( 确定小数点 位置分割整 数小数) | 尾数(整数部分+小数部分) |
float | 首位 | 8 | 23 |
double | 首位 | 11 | 52 |
二进制转十进制
1)读取首位判断0,1,0表示为正数反之负数
2)读取阶位计算阶位值,并将该值减127(float)或者 1023 (double),所得值为小数点偏移量(负数为向左,正数为向右)
备注:这里有个减去固定值的处理,原因是,阶码部分的计算是无符号(unsigned)的,系统设计为正数,所以计算出来的值还要减一个固定值才能得到真实值
3)读取尾数部分假定为a,拼接一个1.a
备注:由于尾数部分最高位固定为1,占据一个位是浪费的,所以存储的时候默认是去除的,计算的时候默认加上
4)根据2)结果移动小数点
5)小数点左边为整数位,右边为小数位,分别转化为十进制,得出结果
十进制转二进制(简单描述)
1)整数位小数位分别转为二进制
2)移动小数位保留一位小数,将偏移量加上固定值转化为二进制放在阶码处(注意根据位数补0),小数点右边的内容放在尾数部分(注意根据位数补0)
3)根据正负设置首位
举个float转二进制的例子:
-13.25
整数位13二进制1101
小数位0.01
组合整数和小数1101.001
用二进制科学计数表示1101.001 = 1.101001*2^3
1.101001*2^3偏移量为3
计算阶码3+127 = 130二进制10000010
根据表格 阶码 8位无需补0即10000010
计算尾数1.101001抹去小数点以及最高位1得101001
尾数23位在末尾补0得尾数10100100000000000000000
-13.25位负则最高位为1
结果1 10000010 10100100000000000000000
double同样如此,只是固定值不再是127
问题:尝试将11000001010100100000000000000000逆推回float,你会吗?
三、范围和精度
float和double的整型
类型 | 范围 | 精度 |
float | 范围是由阶码的最大值决定的,前提是尾数全部为1,阶码的最大值理论上来说是11111111,十进制255-127=128,实际测试的时候发现阶码为11111111的时候该浮点数nan,所以阶码最大值为127。计算十进制最大值2^127+2^126+2^125+......+2^105+2^104,根据数学定律,该值约等于2^128,故范围-2^128~2^128. | 浮点数在计算机中是以二进制表示的抽象科学计数法,其精度由其尾数长短决定。尾数缺省的部分为1: 1、当转十进制的时候小数点不移位,此时尾数能表达的最小二进制的十进制值是2^-23约为0.0000001,1是表示十进制最小单位,所以精度为小数点后7位 2、小数点需要左移,理论上最小单位2^-24,2^-25递减,但是在科学计数法中,左移的几位还是要移回来的2^-24约为0.00000005,5的倍数是不能表示所有十进制的,所以要乘2,得到 0.0000001,而最后小数点还需要右移动一位,实际的精度为小数点后6位。抽象结论:实际上每次除2,小数点都需要右移一位(*10),小数位数不可能会增长只会递减(除2的速度小于*10) 综上所述:精度为小数点后7位 Tip:浮点数在二进制中以科学计数法存储,所以转化为十进制,我们同样以科学计数法的形式描述其精度。 |
double | -2^1024 ~ +2^1024 | 15位 |
以下插入测试代码,证明阶码11111111不存在(c++)
#include <iostream>
#include <cfloat>
#include <bitset>
using namespace std;
int main()
{
int i = 0xffffffff;
float *f = (float*)&i;
cout << *f << " "<< bitset<32>(i) << endl;
getchar();
return 0;
}
打印结果
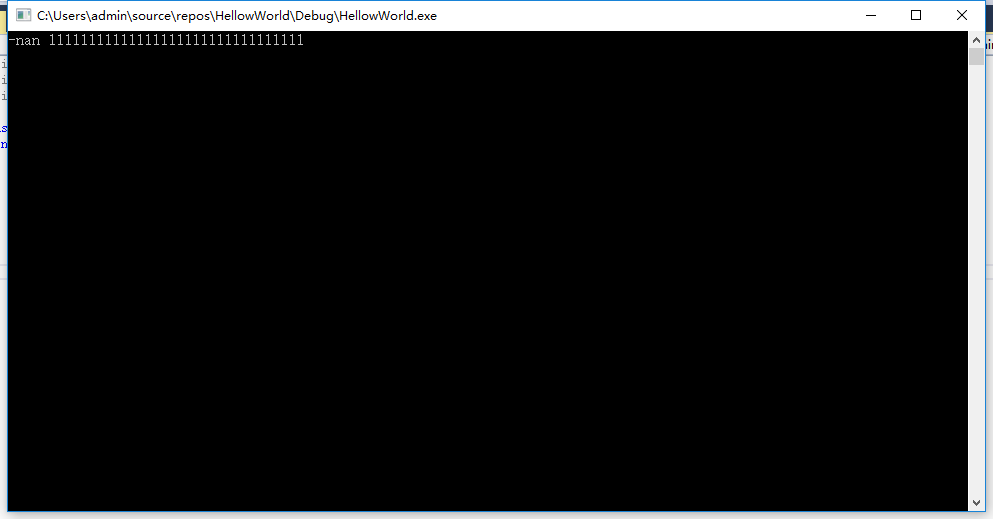
四、无法精确转换二进制的小数
很多朋友可能会发现0.25很好转化为二进制,可是0.2在有限位二进制中是表示不出来的,因为无论怎么*2都很难使小数位为0~~
这种情况下我们系统所做的是根据浮点数类型,一直计算下去知道把尾数的位都占满,float的话是23位:
float类型的0.2=0 10000010 10011001100110011001100
还原过来约为2^-3+2^-4+2^-7=0.1953125(后面很多位省略没计算)
结论:位数越多跟0.2越接近,但无法等于0.2